INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA
INTEGRAL TAK TENTU BERSAMA SIFAT-SIFATNYA BESERTA CONTOH SOALNYA
Jika , maka
Jenis Integral
Seperti yang sudah dijelaskan sebelumnya, terdapat 2 Jenis Integral, yaitu: Integral Tak Tentu dan Integral Tentu
Integral Tak Tentu
Integral Tak Tentu adalah pengintegralan fungsi apabila turunannya telah diketahui.
Integral Tak Tentu Fungsi Aljabar
Rumus
Berikut ini Rumus dari Integral Tak Tentu
Keterangan
= persamaan kurva
= luasan di bawah kurva f`(x)
= konstanta
Sifat
Pada integral tak tentu berlaku sifat berikut
Soal 1
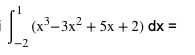
Dalam soal ini, batas atas adalah 1 dan batas bawah -2. Tahap pertama yang perlu kita lakukan adalah melakukan integral fungsi 3x2 + 5x + 2 menjadi seperti di bawah ini.
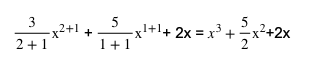
Setelah kita mendapatkan bentuk integral dari fungsi tersebut, kita dapat memasukkan nilai batas atas dan bawah ke dalam fungsi tersebut lalu mengurangkannya menjadi seperti berikut.
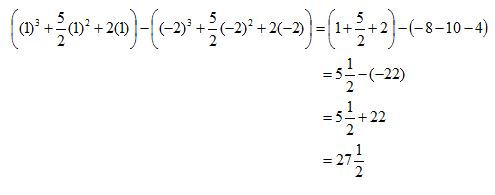
Hasil dari integral tersebut adalah 27,5.
Soal 2.
Diketahui turunan y = f(x) adalah = f ‘(x) = 2x + 3
Jika kurva y = f(x) lewat titik (1, 6), maka tentukan persamaan kurva tersebut.
Jawab:
f ‘(x) = 2x + 3.
y = f(x) = ʃ (2x + 3) dx = x2 + 3x + c.
Kurva melalui titik (1, 6), berarti f(1) = 6 hingga dapat di tentukan nilai c, yakni 1 + 3 + c = 6 ↔ c = 2.
Maka, persamaan kurva yang dimaksud yaitu:
y = f(x) = x2 + 3x + 2.
Soal 3.
Carilah hasil dari ʃ21 6x2 dx !
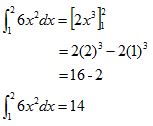
Jadi, hasil dari ʃ21 6x2 dx adalah 14.
SOAL 4
Selesaikan Integral berikut ini.
Jawaban
4. Tentukan hasil dari ʃ 3x2 dx
(3x-2)(x+6) = 3x2 + 18x – 2x -12 = 3x2 + 16x -12
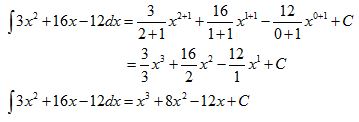
Jadi, hasil dari ʃ (3x-2)(x+6) dx adalah x3 + 8x2 – 12x + C.
DAFTAR PUSTAKA
https://www.edura.id/blog/matematika/integral/
https://www.seputarpengetahuan.co.id/2020/05/integral-tak-tentu.html#Contoh_Soal_Integral



