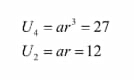Rahmat Abadan Gasalba
(29) XI IPS 2
BARISAN GEOMETRI
Barisan
geometri merupakan barisan bilangan yang hasil bagi antara dua suku
berurutannya selalu sama atau tetap. Perbandingan (hasil bagi) antara
dua suku berurutan pada barisan geometri disebut dengan rasio yang
dilambangkan dengan r.
1. Bentuk barisan geometri
Rumus untuk menentukan rasio pada barisan geometri adalah sebagai berikut.
Keterangan:
r = rasio;
Un = suku ke-n;
Un-1= suku sebelum suku ke-n; dan
n = banyaknya suku.
2. Suku ke-n barisan geometri
Suku
ke-n masih bisa kamu tentukan selama nilai n belum terlalu besar.
Namun, jika nilai n cukup besar, cara seperti itu sulit untuk dilakukan.
Untuk memudahkan kamu dalam menghitung suku ke-n barisan geometri,
gunakan persamaan berikut
Akibat dari rumus suku ke-n tersebut, dapat diperoleh
Jika banyak suku (n) ganjil, suku tengah (Ut) barisan geometri dapat dirumuskan sebagai berikut.
Sementara itu, jika di antara dua buah suku
U1,U2,U3,…,Un disisipkan k buah bilangan sehingga terbentuk barisan
geometri baru, rasio dan banyak suku dari barisan tersebut akan berubah
sesuai rumusan berikut.
Keterangan:
r’= rasio barisan geometri baru;
r= rasio barisan geometri lama;
k= banyak suku yang disisipkan;
n’= banyak suku barisan geometri baru; dan
n= banyak suku barisan geometri lama.
Perlu diingat bahwa suku pertama barisan baru sama dengan suku pertama barisan lama.
Dengan a merupakan suku pertama atau U1. Untuk mengasah kemampuanmu, simak contoh soal berikut ini.
Contoh soal
Diketahui
suku ke-2 dan ke-4 barisan geometri berturut-turut adalah 12 dan 27.
Jika nilai r > 0, tentukan nilai dari suku ke-3!
Pembahasan:
Diketahui:
U2 = 12
U4 = 27
r > 0
Ditanya: U3 =…?
Pembahasan:
Nyatakan suku ke-2 dan ke-4 dalam notasi matematis.
Lakukan pembagian antara kedua suku seperti berikut.
Setelah rasio diketahui, tentukan suku ke-3nya.
Jadi, nilai dari suku ke-3 adalah 18.
3. Suku tengah barisan geometri
Sama
halnya barisan aritmetika. Pada barisan geometri yang banyak sukunya
ganjil, suku tengahnya bisa diperoleh dengan persamaan berikut.
4. Sisipan pada barisan geometri
Misalkan
kamu menjumpai barisan geometri dengan rasio r. Lalu, barisan geometri
tersebut disisipi k bilangan di setiap 2 bilangan yang berdekatan.
Setelah disisipi k bilangan, terbentuk barisan geometri baru yang
rasionya k’. Pertanyaanya adalah berapakah rasio barisan geometri yang
baru? Untuk memudahkan kamu, gunakan persamaan berikut.
DERET GEOMETRI
Jumlah
suku ke-n pertama dari suku-suku barisan geometri disebut sebagai deret
geometri berhingga. Secara matematis, jumlah suku ke-n pertama barisan
geometri dirumuskan sebagai berikut.
Agar belajarmu lebih pas, simak contoh soal terkait deret geometri berikut.
Contoh soal
Pembahasan:
Diketahui:
Ditanya: r =…?
Pembahasan:
Pertama, kamu harus mencari suku pertama dan kedua barisan tersebut.
Selanjutnya, tentukan jumlah 2 suku pertama barisan geometri tersebut.
Tentukan suku ke-2nya.
Tentukan rasionya!
Jadi, rasio barisan geometri tersebut adalah 3.
Contoh soal
Kamu
berinvestasi sebesar Rp10.000.000. Pada bulan pertama kamu investasi,
keuntungan yang diperoleh adalah Rp2.000. Pada bulan kedua,
keuntungannya menjadi Rp4.000 dan bulan ketiga menjadi Rp8.000.
Kira-kira berapa keuntungan yang kamu dapatkan setelah 10 bulan
berinvestasi? Dan berapa total uang yang bisa kamu kumpulkan setelah
berinvestasi selama 10 bulan?
Pembahasan:
Pada
kondisi tersebut, keuntungan setiap bulan merupakan kelipatan 2 dari
bulan sebelumnya. Artinya, jika dibentuk barisan, keuntungan tersebut
akan menjadi barisan geometri, yaitu Rp2.000, Rp4.000, Rp8.000, …,Un.
Setelah 10 bulan, keuntungannya akan menjadi:
Jadi, keuntungan yang akan kamu dapatkan setelah
berinvestasi selama 10 bulan adalah Rp2.046.000 dengan total uang
mencapai Rp10.000.000 + Rp2.046.000 = Rp12.046.000.
Daftar pusaka :
https://www.quipper.com/id/blog/mapel/matematika/barisan-dan-deret-matematika-kelas-11/
