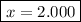SOAL TRANSFORMASI TRANSLASI, REFLEKSI

SOAL TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI DENGAN MATRIKS

SOAL TRANSFORMASI TRANSLASI, REFLEKSI, ROTASI, DILATASI DENGAN MATRIKS UNTUK MENCARI BAYANGANNYA: TITIK, GARIS, BIDANG DATAR, DAN RUANGAN

Assalamualaikum Warahmatullahi wabarakatuh.

 

Rahmat Abadan Gasalba (28) 

Contoh 1

Pencerminan terhadap sumbu x adalah A, pencerminan terhadap sumbu y adalah B dan rotasi 180o terhadap puasat O adalah H. Tentukan matriks B(A(HA)).

Pembahasan:

Diketahui:

•Pencerminan terhadap sumbu

•Pencerminan terhadap sumbu

• Rotasi 180°

Maka:

Contoh 2

Persamaan peta garis 3x – 4y = 12, karena refleksi terhadap garis y – x = 0, dilanjutkan oleh 

transformasi yang bersesuaian dengan matriks \left(\begin{array}{rr} -3&5\\ -1&1\end{array}\right) adalah… (UAN ’03)

Pembahasan 1:

Diketahui matriksnya:

Rotasi =

Transformasi = 

Persamaan garis direfleksi kemudian ditransformasi adalah:

Kemudian disubstitusikan:

Hasilnya:

Contoh 3 

Bayangan titik P jika dicerminkan terhadap sumbu x adalah (4, -2 ). Koordinat titik P adalah ...

Dari persamaan matriks diatas kita peroleh

4 = x → x = 4

-2 = -y → y = 2

Jadi, koordinat titik P adalah (4, 2)  

Contoh 4

Pembahasan:

Mencari nilai a dari transformasi P:

Sehingga matriksnya:

Mencari titik Q:

Sehingga:

Contoh 5 

Hasil pencerminan garis x – 2y – 2 = 0 terhadap sumbu y dan kemudian diputar dengan R[ O(0,0), 90o ] adalah ….

Pembahasan:

Hasil transformasi pencerminan terhadap sumbu y adalah:

Sehingga diperoleh x’ = – x dan y’ = y, selanjutnya substitusikan kedua nilai yang diperoleh pada persamaan x – 2y – 2 = 0.

x – 2y – 2 = 0

– x’ – 2y’ – 2 = 0

Transformasi selanjutnya adalah rotasi sebesar 90° yang berpusat di O(0, 0):

Substitusi nilai x’ = y’’ dan y’ = – x’’ pada persamaan –x’ – 2y’ – 2 = 0, akan diperoleh

– x’ – 2y’ – 2 = 0

– y’’ – 2(–x’’) – 2 = 0

– y’’ + 2x’’ – 2 = 0

2x’’ – y’’ + 2 = 0

Jadi, hasil pencerminan garis x – 2y – 2 = 0 terhadap sumbu y dan kemudian diputar dengan R[ O(0,0), 90o ] adalah 2x – y + 2 = 0.

Bayangan garis y = 2x + 1 oleh rotasi dengan pusat O sebesar 180° adalah ...

Jawab :

Dari persamaan matriks diatas diperoleh

x' = -x → x = -x'

y' = -y → y = -y

Substitusi x = -x' dan y = -y' ke garis y = 2x + 1

-y' = 2(-x') + 1

-y' = -2x' + 1

y' = 2x' - 1

Jadi, bayangannya adalah y = 2x - 1

Contoh 7 

Dilatasi yang berpusat di titik (3, 1) dengan faktor skala 3, memetakan titik (5, b) ke titik (a, 10). Maka nilai a – b adalah ….

Pembahasan:

Dilatasi dengan pusat (3, 1) dengan faktor skala 3 akan menghasilkan matriks transformasi berikut.

Contoh 8 

Hasil translasi titik P1(3, –2) oleh T1 dilanjutkan dengan T2,

Mencari nilai b:

-2 + b + 1 = 7

b – 1 = 7

b = 7 + 1 = 8

Jadi, nilai translasi dari T1 adalah

Contoh 10

Tentukan bayangan segitiga ABC dengan koordinat titik-titik A(2,3), B (8,3) dan C (8,-2) jika ditranslasikan oleh vektor translasi: T(2,-3). 

Perhatikan hasil bayangan segitiga yang kalian peroleh:

a) Bagaimana bentuk segitiga bayangan tersebut jika dibandingkan dengan segitiga ABC? 

b) Apakah luas kedua segitiga tersebut sama? Jelaskan dengan perhitungan matematika! 

Pembahasan: 

Titik A (2,3), Titik B (8,3), Titik C (8,-2)

 Kemudian semua titik ditranslasikan 

T(2,-3) Titik A (2+2), (3-3), A'(4,0) 

Titik B (8=2), (3-3), B'(10,0) 

Titik C (8+20, (-2,-3), C'(10,-5) 

a) Bentuk dan ukuran bayangan segitiga sama persis dengan titik segitiga semula. 

b) Luas kedua segitiga tersebut sama besar karena panjang sisi-sisinya juga sama besar. 

Perhitungan Matematikanya Luas segitiga = Luas bayangan yaitu L = 1/2.a.t

 DAFTAR PUSTAKA : 

https://idschool.net/sma/rumus-pada-transformasi-geometri-translasi-refleksi-rotasi-dan-dilatasi/

https://www.studiobelajar.com/transformasi-geometri/ 

Tranformasi Translasi, Refleksi, Rotasi dan Dilatasi

Tranformasi Translasi, Refleksi, Rotasi dan Dilatasi

Assalamualaikum wr. wb

Rahmat Abadan Gasalba (28) XI IPS 2

Transformasi Translasi, Refleksi, Rotasi dan Dilatasi dengan gambar balok ABCDEFGH koordinat titik A(0,0), B(4,0), C(4,4), D(0,4), E(10,0), F(14,0), G(14,4), H(10,4) dan perhitungan mendapat bayangannya.

Semoga bermanfaat

Soal cerita dengan penyelesaiannya gunakan invers dan determinan matriks

Nama: Rahmat Abadan Gasalba

Absen: 28

Kelas: XI IPS 2

1. Roni membeli 5 pensil dan 3 penghapus, sedangkan Yogi membeli 4 pensil dan 2 penghapus di toko yang sama. Di kasir, Roni membayar Rp 11.500,00 sedangkan Yogi membayar Rp 9.000,00. Jika Karim membeli 6 pensil dan 5 penghapus, berapa ia harus membayar?

Persoalan ini dapat diselesaikan menggunakan dua cara. Jika

maka. 

dengan cara pertama, yakni cara invers, diperoleh 

Ingat, determinan dari

adalah ad - bc.

Penyelesaian cara kedua adalah cara determinan, yaitu:

Penyelesaian

Dimisalkan harga satuan pensil = x dan harga satuan penghapus = y. Disusun ke dalam sistim persamaan linear dua variabel (SPLDV)

5x + 3y = 11.500

4x + 2y = 9.000

Sistim persamaan di atas dapat dinyatakan dalam bentuk matriks, yakni

Cara Pertama (Invers Matriks)

dan

Diperoleh harga satuan pensil Rp 2.000 dan harga satuan penghapus Rp 500.

Jadi, Karim harus membayar [6 x Rp 2.000] + [5 x Rp 500] = Rp 14.500

2. Umur pak Usman 28 tahun lebih tua dari umur Amel. Umur bu Nur 6 tahun lebih muda dari pak Usman. Jika jumlah umur pak Usman, bu Nur dan Amel 119 tahun, maka jumlah umur Amel dan bu Nur adalah....

Pembahasan :

Misal ->

Umur Pak Usman = X

Umur Amel = Y

Umur Bu Nur = Z

Maka ->

X = Y + 28 ( Pindahkan Variabel ke sisi kiri ) X - Y = 28

Z = X - 6 ( Pindahkan Variabel ke sisi kiri ) X - Z = 6

X + Y + Z = 119

Ubah ke bentuk Matriks ->

D ( Determinan ) ->

= ( 0 + 1 + 0 ) – ( 0 - 1 - 1 )

= 1 + 2

= 3

DX ( Determinan X ) ->

= ( 0 + 119 + 0 ) – ( 0 - 28 - 6 )

= 119 + 34

= 153

DY ( Determinan Y ) ->

= ( 6 - 28 + 0 ) – ( 0 - 119 + 28 )

= -22 + 91

= 69

DZ ( Determinan Z ) ->

= ( 0 - 6 + 28 ) – ( 0 + 6 - 119 )

= 22 + 113

= 135

Langkah selanjutnya cari nilai X,Y,danZ

Jadi, jumlah umur Amel dan Bu Nur =

Y + Z = 23 + 45 = 68

Daftar pustaka

https://www.academia.edu/8513445/Soal_Penerapan_Matriks

https://www.ilmusosial.id/2020/06/contoh-soal-cerita-matriks-dan.html