Persoalan dalam program linear yang masih dinyatakan dalam kalimat-kalimat pernyataan umum, kemudian diubah kedalam model matematika. Model matematika merupakan pernyataan yang menggunakan peubah dan notasi matematika.
Sebagai ilustrasi, produsen sepatu membuat 2 model sepatu menggunakan 2 bahan yang berbeda. Komposisi model pertama terdiri dari 200 gr bahan pertama dan 150 gr bahan kedua. Sedangkan komposisi model kedua terdiri dari 180 gr bahan pertama dan 170 gr bahan kedua. Persediaan di gudang bahan pertama 72 kg dan bahan kedua 64 kg. Harga model pertama adalah Rp. 500.000,00 dan model kedua Rp. 400.000,00. Jika disimpulkan/disederhanakan dalam bentuk tabel menjadi berikut:
Dengan peubah dari jumlah optimal model 1 adalah x dan model 2 adalah y, dan hasil penjualan optimal adalah f(x, y) = 500.000x + 400.000y. Dengan syarat:
- Jumlah maksimal bahan 1 adalah 72.000 gr, maka 200x + 180y ≤ 72.000.
- Jumlah maksimal bahan 2 adalah 64.000 gr, maka 150x + 170y ≤ 64.000
- Masing-masing model harus terbuat.
Model matematika untuk mendapat jumlah penjualan yang maksimum adalah:
Maksimum f(x, y) = 500.000x + 400.000y
Syarat:
- 200x + 180y ≤ 72.000
- 150x + 170y ≤ 64.000
- x ≥ 0
- y ≥ 0
Fungsi objektif merupakan fungsi linear dan batasan-batasan pertidaksamaan linear yang memiliki himpunan penyelesaian. Himpunan penyelesaian yang ada merupakan titik-titik dalam diagram cartesius yang jika koordinatnya disubstitusikan kedalam fungsi linear dapat memenuhi persyaratan yang ditentukan.
Nilai optimum fungsi objektif dari suatu persoalan linear dapat ditentukan dengan metode grafik. Dengan melihat grafik dari fungsi objektif dan batasan-batasannya dapat ditentukan letak titik yang menjadi nilai optimum. Langkah-langkahnya sebagai berikut :
- Menggambar himpunan penyelesaian dari semua batasan syarat yang ada di cartesius.
- Menentukan titik-titik ekstrim yang merupakan perpotongan garis batasan dengan garis batasan yang lainnya. Titik-titik ekstrim tersebut merupakan himpunan penyelesaian dari batasannya dan memiliki kemungkinan besar membuat fungsi menjadi optimum.
- Menyelidiki nilai optimum fungsi objektif dengan dua acara yaitu :
- Menggunakan garis selidik
- Membandingkan nilai fungsi objektif tiap titik ekstrim
Menggunakan Garis Selidik
Garis selidik diperoleh dari fungsi objektif f(x, y) = ax + by dimana garis selidiknya adalah
ax + by = Z
Nilai Z diberikan sembarang nilai. Garis ini dibuat setelah grafik himpunan penyelesaian pertidaksamaan dibuat. Garis selidik awal dibuat di area himpunan penyelesaian awal. Kemudian dibuat garis-garis yang sejajar dengan garis selidik awal. Berikut pedoman untuk mempermudah penyelidikian nilai fungsi optimum:
Cara 1 (syarat a > 0)
- Jika maksimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di kiri garis tersebut. Titik yang dilalui garis tersebut adalah titik maksimum.
Jika minimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di kanan garis tersebut. Titik yang dilalui garis tersebut adalah titik minimum.
Cara 2 (syarat b > 0)
- Jika maksimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di bawah garis tersebut. Titik yang dilalui garis tersebut adalah titik maksimum.
- Jika minimum, maka dibuat garis yang sejajar garis selidik awal sehingga membuat himpunan penyelesaian berada di atas garis tersebut. Titik yang dilalui garis tersebut adalah titik minimum.
Untuk nilai a < 0 dan b < 0 berlaku kebalikan dari kedua cara yang dijelaskan di atas.
Membandingkan Nilai Fungsi Tiap Titik Ekstrim
Menyelidiki nilai optimum dari fungsi objektif juga dapat dilakukan dengan terlebih dahulu menentukan titik-titik potong dari garis-garis batas yang ada. Titik-titip potong tersebut merupakan nilai ekstrim yang berpotensi memiliki nilai maksimum di salah satu titiknya.
Berdasarkan titik-titik tersebut ditentukan nilai masing-masing fungsinya, kemudian dibandingkan. Nilai terbesar merupakan nilai maksimum dan nilai terkecil merupakan nilai minimum.
Contoh Soal Program Linear dan Pembahasan
Tentukan nilai minimum f(x, y) = 9x + y pada daerah yang dibatasi oleh 2 ≤ x ≤ 6, dan 0 ≤ y ≤ 8 serta x + y ≤ 7
Pembahasan 1:
- Langkah 1 menggambar grafiknya
- Langkah 2 menentukan titik ekstrim
Dari gambar, ada 4 titik ekstrim, yaitu: A, B, C, D dan himpunan penyelesaiannya ada di area yang diarsir.
- Lankah 3 menyelidiki nilai optimum
Dari grafik diketahui titik A dan B memiliki y = 0, sehingga kemungkinan menjadi nilai minimum. Kedua titik disubstitusikan kedalam f(x, y) = 9x + y untuk dibandingkan.
Dengan membandingkan, disimpulkan titik A memiliki nilai minimum 18
Contoh Soal 2
Tentukan dimana nilai maksimum fungsi f(x, y) = 4x + 5y yang akan dicapai pada pada grafik ini!
Pembahasan 2:
Titik ekstrim pada gambar adalah:
- A tidak mungkin maksimum karena titik paling kiri.
- B(3, 6)
- C(8, 2)
- D(8, 0)
Nilai tiap titik ekstrim adalah:
Sehingga nilai maksimum ada pada titik yang melalui garis BC dengan nilai maksimum 42.
Contoh Soal 3
Pedagang buah memiliki modal Rp. 1.000.000,00 untuk membeli apel dan pisang untuk dijual kembali. Harga beli tiap kg apel Rp 4000,00 dan pisang Rp 1.600,00. Tempatnya hanya bisa menampung 400 kg buah. Tentukan jumlah apel dan pisang agar kapasitas maksimum.
Pembahasan 3:
Diketahui:
Dengan syarat:
- Kapasitas tempat: x + y ≤ 400
- Modal: 4.000x + 1.600y ≤ 1.000.000
- x ≥ 0
- y ≥ 0
Diagramnya:
Titik ekstrim:
- A(0, 400) bukan optimum karena tidak ada apel
- C(250, 0) bukan optimum karena tidak ada pisang
dengan metode eliminasi 2 persamaan diatas diperoleh:

Sehingga jumlah masimum:
- Apel: 150 kg
- Pisang: 250 kg
Biaya produksi satu buah payung jenis A adalah Rp20.000,00 per buah, sedangkan biaya satu buah produksi payung jenis B adalah Rp30.000,00. Seorang pengusaha akan membuat payung A dengan jumlah tidak kurang dari 40 buah. Sedangkan banyaknya payung jenis B yang akan diproduksi minimal adalah dari 50 buah. Jumlah maksimal produksi kedua payung tersebut adalah 100 buah. Biaya minimum yang dikeluarkan untuk melakukan produksi kedua payung sesuai ketentuan tersebut adalah ….
A. Rp2.000.000,00
B. Rp2.300.000,00
C. Rp2.200.000,00
D. Rp2.100.000,00
E. Rp2.000.000,00
Pembahasan:
Pemisalan:
- x = banyak payung A
- y = banyak payung B
Model matematika dari permasalahan tersebut adalah:
Fungsi tujuan: meminimumkan f(x,y) = 20.000x + 30.000y
Fungsi kendala:
- x ≥ 40
- y ≥ 50
- x + y ≤ 100
Daerah penyelesaian yang memenuhi permasalahan:
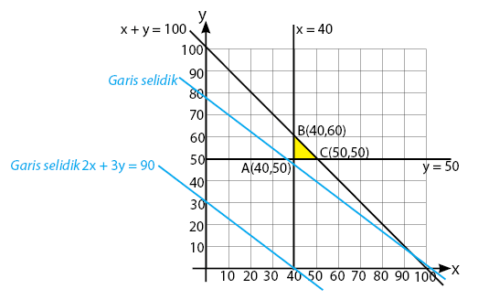
Nilai minimum akan diperoleh melalui titik koordinat yang dilalui garis selidik yang pertama kali, yaitu titik A(40, 50).
Sehingga, biaya produksi minimum adalah
f(40,50) = 20.000(40) + 30.000(50)
f(40,50) = 800.000 + 1.500.000
f(40,50) = 2.300.000











